cubingpro.com

Back to Home

Yau method for big cubes

Introduction

Yau method is a very popular speedsolving method for big cubes (4x4x4, 5x5x5, 6x6x6, 7x7x7).

The steps for Yau4 method and Yau5+ method are very similar, with some adjustment needed.

It's highly recommended to learn the redux (reduction) method first, which reduce a big cube into a 3x3x3 cube, and then apply normal 3x3x3 methods, and optionally handles special cases called parity (cases that would not appear for 3x3x3 cube, but possible on big cubes).

The Yau method consists of the following steps:

1. Solve centers of two opposite colors
2. Solve three edges on the color you plan to do cross with, called cross edges
3. Solve the remaining four centers while preserving the three cross edges
4. Solve the last cross edge
5. Solve the last 8 edges (this is where Yau4 and Yau5+ differs)
6. Solve the 3x3 stage and edge parity

For this tutorial, we assume white is the cross color.

Yau Method for 4x4x4

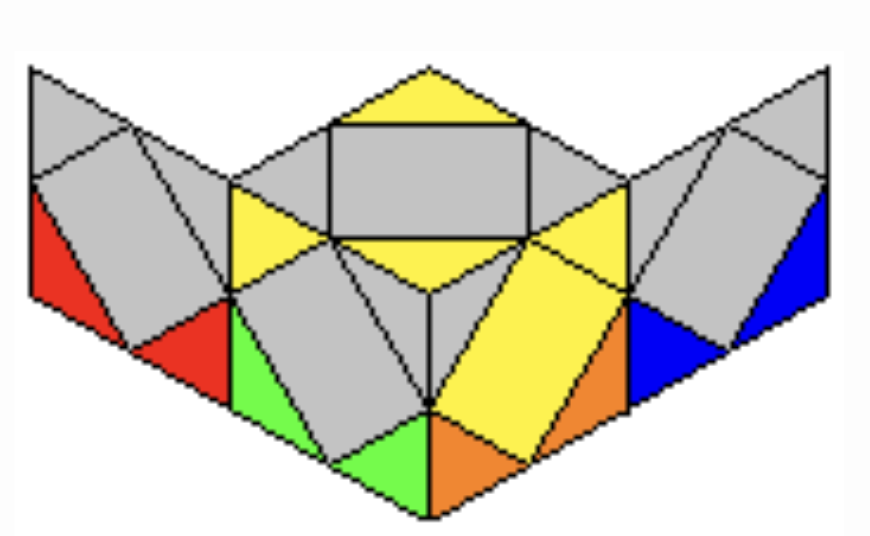
Step 1: Solve centers of two opposite colors

Step 2: Solve three cross edges

During this step, you should put the cross center on your left.

Note the three cross edges should be in correct relative order: e.g. for white cross, blue followed by orange, followed by green, in x' order.

There are tutorials which advice on solving cross edges while deliberately put an edge in incorrect order and eventually fix that during step 4, but it's not recommended because of the hindering on solving flow.

This step is intuitive, make sure to utilize the fact that only two centers are already solved, and you may be very flexible during the solve.

For example, you may use Rw U x' to solve the white-red cross edge.

Step 3: Solve the centers

This step is very similar to solving centers in traditional redux method.

After this step, we have solved all centers and 3 cross edges.

Note that the centers and cross edges do not need to be aligned (can be shifted). The alignment will be done in next step.

The only thing is to make sure your solution of the center does not break the cross edges.

Note that for 4x4x4, lot of the center algorithms are triggers in the form of wide move, U/U'/U2, wide move.

If the wide move is Rw, e.g. Rw U2 Rw', then this naturally doesn't affect three cross edges (LB, LD, LF).

If the wide move is Lw, e.g. Lw U Lw', then this as-is breaks a cross edge (LB). To avoid this, replace wide move to slice move, e.g. l U l'.

Exercise: what should be the algorithm to solve these last 2 centers? If centers are to be solved, the top should be blue, and the front should be red.

The answer will be U2 l' U2 Rw.

Step 4: Solve last cross edge

After centers and 3 cross edges are solved, we may solve the last cross edge while preserving the centers.

The end state is:

Two cases are very common, you may set up any last cross edge case to one of the two cases (with mirrored algorithm):

Case 1:

The algorithm is Rw U' R' U' R U2 Rw' or Rw F' U' F U Rw'

Case 2:

r U R U' Rw' U

Notice that you don't have to solve the last cross edge with center aligned at cross edge, but you should align them after pairing the last cross edge.

Step 5: Solve the last 8 edges

There are two substeps:

1. Solve three edges using a slice
2. Solve the last 5 edges

This step is identical to that of the standard reduction method.

For substep 1,

first make an Uw move, then insert edge at right slot and rotate cube with y', for three times.

For example, to pair FR edge's bottom wing with FL edge's top wing, you may apply R U' R'. Then y' and try to pair the new FR bottom wing to new FL top wing (old FR top wing).

After inserting three times, apply a Uw' move, which will solve three edges except for one.

Now move on to substep 2,

the idea is the same, keep unsolved edge at FL. Then insert an edge to pair with the top wing of FL.

The next step is very intuitive: Uw' to pair these two wings, then insert an edge to pair with the top wing of FR (now at top wing of BR), apply Uw.

This paradigm solves 2 edges.

Optionally, you may have exactly 2 edges unsolved at the end. There are L2E algorithms available, but you may start with learning the following algorithm. Insert the other unsolved edge from top layer to FR, then apply this algorithm:

Uw' R U R' F R' F' R Uw

Step 6: Solve the 3x3 stage and edge parity

Since the cross is already solved, you may start from F2L directly.

The rest on parity is same as the redux method.

Some helpful tips are:

• Start inspecting F2L during step 5 to avoid a long pause at this step.
• Try to identify OLL parity during the last F2L solve to reduce pausing.
• Polish parity algorithms' fingertrick.

Yau Method for 5x5x5

We will skip the part that is identical to Yau 4x4x4, and focus on the unique parts for Yau5.

Step 5: Solve the last 8 edges

Instead of using a slice to pair up 3 edges first, the Yau5 L8E follows:

1. Repeat 4 times: put three wings of an edge on E layer and align them with Uw and Dw moves, then insert an unsolved top edge (which aligns with unsolved wings as the start of next step) which automatically sends this solved edge to the top layer. Make sure there are at least 2 E-layer edges that are solved during this step, by picking at least 2 of them deliberately.
2. Solve 2 F2L pairs for the solved E-layer edges. If the two pairs are diagonal, then apply a single R' move or R move so that the unsolved E-layer edges are on the same face (rotate it to the front).
3. Pair the rest of edges one by one using standard edge pairing.
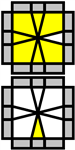
4. Solve the L2E which is similar as redux. You may start with solving one edge, and optionally (if parity occurs) send the parity edge to the top layer then apply OLL parity algorithm for the last edge.

Step 6: Solve the 3x3 stage and edge parity

There will be no parity for Yau5 due to the nature of 5x5x5 cube, and parity was guaranteed to be solved during edge pairing (step 5).

There is another variant of Yau 5x5x5 step 5, which doesn't enforce two E-layer edges, consider learning that as an alternative approach and experiment which one works best for you.

Yau Method for 6x6x6

Yau6 is almost identical to Yau5.

The only point worth mentioning is the L2E.

In Yau6, you may first solve one of the edge, and try to influence the solving order through the process so the last (maybe) unsolved edge is a top edge.

The benefit is that you may leave that unsolved edge remains unsolved until the 3x3x3 stage's last layer, in which you identify whether an inner layer parity should be applied or an outer layer parity should be applied, or there's no OLL parity.

This trick avoids triple parity where you solve the edge parity during L2E, then get OLL parity, and PLL parity during the 3x3x3 stage.

Yau Method for 7x7x7

Yau7 method is identical to Yau5.

The only point worth mentioning is still the L2E.

You may solve one of the L2E first, then apply a potential parity algorithm for the last one edge (because there will be no parity during 3x3x3 stage).

One tip to consider for Yau6 and Yau7 is to stick with solving the 4 E-layer edges first, the motivation is to have more options and less reaction time for the first two F2L step, and also simplify the inspection during the L4E stage. It also guarantees the parity edge will be for sure a top layer edge, so you may leave it at the very end of the 3x3x3 stage for both Yau6 and Yau7.

The drawback however is you might miss very easy top-layer edge cases, so be a little flexible when you observe very easy top-layer edge, and practice more to improve weighing the tradeoffs.