cubingpro.com
7 Simul Flip Theory
Here we present the proof of the above solution, by formulating the problem of solving Rubik's clock as solving a
linear algebra equation.
We will explain how to formulate the problem as a matrix equation, with the example of filling only a few row
entries in the matrix.
The entries could also be computed using a computer program.
Problem formulation
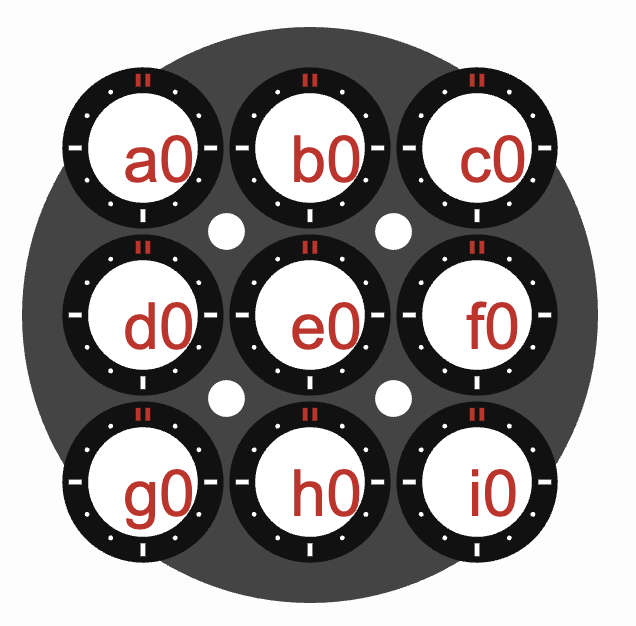
Denote initial values of the clock as a0, b0, c0, d0, ...
There are 14 operations in 7 simul flip method. In step 1, we execute left dial (operation 1), then right dial
(operation 2). In step 2, we execute left dial (operation 3), then right dial (operation 4) ...
We annotate the clockwise turn count on each operation. If we turn more than 180 degrees clockwise, annotate as a
negative.
For example, if we turn left dial at first step by 60 degrees counterclockwise, then x1 = -2.
If we turn right dial at first step by 120 degrees clockwise, then x2 = 4.
Let's consider the effect of applying x1 move(s) onto the clock value.
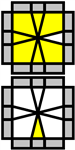
See the visualilzation below of how would one clockwise move affect the clocks.
We know that clock a will be incremented by 1, clock b will be incremented by 1, etc.
Therefore, after applying x1 moves(s), the clock become:
After applying all the moves, clock a will become a0 + a linear combination of x1, x2, ...
We could either derive these linear combinations by manually tracing the effect of each move, or with a computer program.
Eventually, we want to find a solution of x1, x2, ..., x14, such that each clock become 0.
If you are familiar with linear algebra, this could be represented as an equation:
$$ \begin{bmatrix} a_0 \\ b_0 \\ c_0 \\ \vdots \\ n_0 \end{bmatrix} + T \cdot \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_{14} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} $$
Notice T is a 14x14 matrix, and it happens to be invertible.
$$ \Rightarrow \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_{14} \end{bmatrix} = -T^{-1} \cdot \begin{bmatrix} a_0 \\ b_0 \\ c_0 \\ \vdots \\ n_0 \end{bmatrix} $$
If we denote $$ S = -T^{-1} $$, then $$ x_1 = S_{1,1}a_0 + S_{1, 2}b_0 + \cdots + S_{1, 14}n_0 $$ In other word, each $$x_i$$ is a linear combination of $$a_0, b_0, \cdots, n_0$$ The solution after cleaning up will be the results presented in 7sf+ and speed BLD
Further reading
Here are some websites with other fun theories: